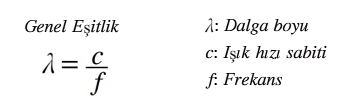Alice Yasası Versiyon 7 Alanlar ve (c+v)(c-v) matematiği

Alice Yasası Versiyon 7

Doppler Efekti

Han Erim

7 Mayıs 2012

DOPPLER EFEKTİ

(c+v)(c-v) matematiğinin fizikte hiç kullanılmadığını ve yalnızca Alice Yasasına özel, ona has bir matematik olduğunu düşünebilirsiniz ancak bu doğru değildir. (c+v)(c-v) matematiği mevcut fiziğin içinde çok önemli bir yerde kendi varlığının izini bize gösterir. Bu yer Doppler Efektidir.

Doppler Efekti hareketli cisimlerden gelen elektromanyetik dalgalar üzerinde görülen bir etkidir ve ışığın dalga boyundaki değişim olarak tanımlanır.

Doppler Efekti Elektromanyetik Teoride tam olarak anlaşılamamış bir konudur. Bunun nedeni daha önce söylediğim gibi Elektromanyetik Teorinin kurulumunda hata yapılmış olması ve matematiğinin eksik kalmış olmasıdır. Elektromanyetik Teori kendisine (c+v)(c-v) matematiği temel alması gerekirken bunu yapmamıştır. Bu eksiklik nedeniyle de Doppler Efekti gibi önemli bir konu tam olarak anlaşılamamıştır. Bununla beraber Doppler Efekti formüle edilirken mecburen (c+v)(c-v) matematiği kullanılmıştır. Çünkü Doppler Efekti (c+v)(c-v) matematiği ile direk ilişkilidir ve onun haricinde başka bir matematikle açıklanamaz. Yani Elektromanyetik Teori burada ister istemez, kendi matematiği ile uyumsuz bile olsa (c+v)(c-v) matematiğini kullanmak zorunda kalmıştır.

Alice Yasası Doppler Efektini daha oluşum nedeninden başlayarak açıklar. Aslına bakarsanız Doppler Efektinin varlığı (c+v)(c-v) matematiğinin deneysel doğrulamasıdır da denilebilir. Burada Doppler Efektini Alice Yasasının penceresinden bakarak göreceğiz.

Doppler Efekti Nedir?

Doppler Efekti ses ve elektromanyetik dalgalar üzerinde görülür. Ancak oluşum mekanizması ses ve elektromanyetik dalgalarda farklıdır. Burada yalnızca elektromanyetik dalgalar üzerinde görülen Doppler Efektini anlatacağım.

Bir elementin hangi dalga boylarında ışıdığı bellidir. Özellikle astronomide yıldızların yapısı incelenirken yıldızın hangi dalga boylarında ışık yaydığı araştırılır. Bu araştırmanın sonucunda yıldızın hangi elementlerden oluştuğu, elementlerin bulunma yoğunluğu gibi çeşitli bilgiler elde edilir. Yıldızdan elde edilen dalga boyları, standart dalga boyu cetveli ile karşılaştırıldığında aynı elementlere ait dalga boyları arasında genellikle bir fark görülür. Gözlemlenen yıldız eğer uzaklaşan bir yıldız ise elemente ait dalga boyları büyümekte (REDSHIFT) (sağdaki resim), yaklaşan bir yıldız ise dalga boyları küçülmektedir (BLUESHIFT). Dalga boyundaki bu değişime, bu etkiyi tespit edip fiziğe uyarlayan Christian Doppler'in anısına Doppler Efekti adı verilmiştir.

Bugün artık, Doppler Efektinin birbirine göre hareketli bütün frameler arasında gerçekleştiğini ve bütün dalga boylarını kapsadığını biliyoruz.

Elektromanyetik Spektrum

Elektromanyetik dalgaların spektrumu son derece geniştir. Dalga boyları teorik olarak sıfır ile sonsuz arasında değişebilir. Yandaki tabloda dalga boyuna ve frekansına göre elektromanyetik dalgaların sınıflandırılmasını görüyoruz.

Gözlerimiz bu geniş spektrum aralığı içinde çok küçük bir dalga boyu aralığına karşı duyarlıdır. Bu aralığa görünür ışık diyoruz. Göremediğimiz bazı dalga boylarını ise bildiğiniz gibi haberleşmede, tıpta, ısıtmada ve başka bir çok uygulama alanında kullanıyoruz.

Elektromanyetik dalgalar için dalgaboyu ve frekans arasında aşağıdaki genel eşitlik vardır. Bu eşitliğin nedenini konunun ilerleyen kısmında göreceğiz.

Figür 1 Doppler Efekti buradaki animasyona çok benzer bir şekilde gerçekleşir.

Animasyonda rulo halinde hareketli bir kağıt vardır. Kağıdın hızını kontrol edebiliyoruz. Kalem sabit bir hızda aşağı ve yukarı sabit bir frekansta salınmaktadır ve hemen altındaki hareketli kağıdı çizmektedir.

Çizginin şekli kağıdın hızına bağlı olarak değişecektir.

Yatay yöndeki hareketler için, kalem dururken kağıdın hareket etmesi veya kalem giderken kağıdın durması tamamen benzer sonuç verir.

Figür 2, Doppler Efekti

Bir önceki animasyonu burada elektromanyetik dalgalarla yapılmış şekilde görüyoruz. Burada kalem yerine bir mıknatıs vardır. Mıknatıs düzgün bir şekilde titreşmektedir. Bu titreşimler elektromanyetik dalgalar halinde uzaygemisinin alanı tarafından uzaygemisine iletilmektedir.

Alan üzerine oluşan her etki c (ışık hızı sabiti) hızıyla uzay gemisine doğru gider. Burada c hızı elektromanyetik dalganın alana göre olan hızıdır. Uzay gemisinin hareket yönü ve hızı elektromanyetik dalganın alana göre olan hızını değiştirmez. Ama öte yandan uzay gemisinin hızı ve yönü mıknatısın çizdiği çizginin şeklini değiştirir (elektromanyetik dalgalar değişime uğrar). Çünkü uzay gemisi kendi alanını kendisiyle birlikte beraber taşımaktadır. Çizginin şeklinin değişmesi gördüğümüz gibi dalga uzunluğunun değişmesi şeklinde olmaktadır. Uzaygemisi hareket halindeyse, kendisine varan elektromanyetik dalganın boyunun normalden farklılaştığını görecektir, yani bir Doppler etkisi gözlemler. Doppler Etkisinin kaynakta (mıknatıs tarafında) elektromanyetik dalga yayınlanırken oluştuğuna dikkat edelim.

Görüldüğü gibi uzaygemisinin kaynağa doğru gitmesi halinde dalga boyları küçülmekte (BLUSHIFT), uzaygemisinin kaynaktan uzaklaşması durumunda dalga boyları uzamaktadır (REDSHIFT).

Animasyondaki değerler pixel/saniyedir. Animasyonun gerçekçi olması amacıyla ışık hızı 299.792458 pixel/sn olarak set edilmiştir. Animasyonu doğru yorumlayabilmek için hız değerini set ettikten sonra, bütün dalgaboyları eşit olana kadar bekleyin.

Figür 3, Doppler Efekti

Burada ise bir önceki animasyonun ışık ile yapılmış ve biraz daha gelişmiş olanını görüyoruz. Doppler Etkisinin oluşumu açısından, gözlemcinin hareket etmesi ve lambanın durması veya lambanın hareket etmesi ve gözlemcinin durması tamamen aynı şekilde sonuçlanır. Zaten temel prensip olarak hangisinin hareket ettiği önemli olmamalıdır.

Işık (foton) bir elektromanyetik dalga olmasına karşın, diğer fotonlardan bağımsız bir enerji paketidir. Dolaysıyla animasyonun en gerçekçi çizimi 4. şıkta olan çizimdir. Elektromanyetik dalgaları frekanslarına göre sınıflandırabildiğimiz için 1. 2. ve üçüncü şıklarla düşünmek de mümkündür.

4. şıkka dikkat edersek, Doppler Etkisinin önemli bir başka sonucunu da görebiliriz. Doppler Etkisi sonucunda gelen ışığın gücü (ışığın lümeni) artmakta veya azalmaktadır. Gözlemci kaynağa doğru yaklaşırken birim zaman içinde gözlemciye varan fotonların sayısı artmakta, gözlemci uzaklaşırken birim zamanda kendisine varan fotonların sayısı azalmaktadır.

Doppler Etkisinin fotonlar üzerinde ikinci bir etkisi daha varır. Gözlemci kaynağa doğru yaklaşırken kendisine gelen fotonlar daha enerjik olur. Uzaklaşırken de tersine bir etki meydana gelir.

Figür 4, (c+v)(c-v) MATEMATİĞİ İLE DALGABOYU VE FREKANS ARASINDAKİ İLİŞKİ

Burada dalga boyu ve frekansın (c+v)(c-v) matematiği ile olan ilişkisini
görüyoruz. Dalga boyu ve frekans üzerindeki değişim (c+v)(c-v) matematiğine direk bağımlıdır.

Figür 5, Dalgaboyu ve Frekans arasındaki ilişki

Figüre bakarsak ışığın alan üzerinde bir dalga boyuna eşit uzunluğu c hızıyla t kadar zamanda kat edeceğini görebiliriz. Yani λ = c. t dir. Burada t süresi t = λ/c olur. Bu t süresi aynı zamanda λ uzunluğundaki bir elektromanyetik dalganın periyodu (T) olmaktadır. Yani t = T dir.
Periyot ile frekans arasında da T =1/f eşitliği vardır. Burada T yerine t yazabiliyoruz. t=1/f . Frekans 1 birim süre içindeki tekrarlanma sayısıdır. λ = c. t eşitliğinde t yerine 1/f koyarsak λ = c. f veya f= λ/c elde edilir.

Sayfanın alt kısımda Doppler Etkisine ait eşitlikleri özet halinde görüyoruz. Bu eşitlikleri bir önceki sayfada elde etmiştik.

Figür 6, Doppler Efekti ve Relativite etkileri arasındaki direk ilişki ve Erim Eşitlikleri

Relativite etkileri olan boyut deformasyonu, zaman uzaması, algılama hızının değişmesi hiçbir zaman tek başlarına var olmazlar. Eğer bir zaman uzaması gerçekleşmişse diğer etkilerde aynı anda oluşmuştur. Bir gözlemde Doppler Etkisinin tespit edilmesi relativite etkilerinin oluştuğuna işaret eder. Çünkü Doppler Etkisinin oluşma nedeni de relativite etkilerinin oluşma nedeniyle aynıdır ve Doppler Etkisi diğer relativite etkileriyle birlikte aynı anda oluşur.

Boy deformasyonu, zaman uzaması ve eşzamanlık bölümlerinde relativite etkilerin nasıl formüle edileceğini zaten görmüştük. Doppler Efekti de aynı matematiksel denklemleri kullandığı için aradaki ilişki kolaylıkla kurulabilmektedir. Yaptığımız bir gözlemde RedShift veya BlueShift tespit etmiş isek diğer relativite etkilerinin hangi oranda gerçekleştiğini dalga boyundaki değişimden yararlanarak kolaylıkla tespit edebiliriz.

Doppler Etkisi ile relativite etkileri arasındaki ilişkiyi fark etmemin sonucunda gördüğünüz bu tablo ortaya çıkmıştır. Tabloya bir ad vermek istedim ve kendi soyadım olan "ERIM" adını verdim.

Tablonun üzerindeki butonları kullanarak her bölümün ilgili sayfalarına gidebilir ve ilişkileri birebir görebilirsiniz.

Dalga boyu ve frekans için maksimum ve minimum limitler.

Doppler efekti belirli limitler içinde gerçekleşir. Bu limitleri belirleyen referans sistemleri arasındaki hız farkının bir limite sahip olmasıdır. Bildiğimiz kadarı ile hiç bir maddesel cismin hareket hızı c ışık hızı limitini aşamamaktadır. Bu konuda farklı varsayımlar üretmek mümkündür ama burada bunları tartışmayacağız.

Maddesel cisimler için c hız limitini prensipte temel aldığımızda iki referans sistemi birbirine göre en fazla c hızı ile yaklaşabilir veya birbirinden en fazla c hızı ile uzaklaşabilir diye düşünebiliriz. Bu durumda (c+v)(c-v) matematiğinde framelerin birbirine göre hız farkını gösteren v değeri +c ve - c limitleri arasında değişecektir (*). Denklemlerde v yerine +c ve -c değerleri konulduğu takdirde maksimum ve minimum limitler elde edilir.

Buna göre bir elektromanyetik dalganın değişme aralıkları:
Dalgaboyu için:
0 ≤ λ ≤ 2 λ

Frekansı için:
ƒ/2 ≤ ƒ ≤ ∞ olmaktadır.

Frekanstaki ve dalga boylarındaki bu değişim limitlerini zaten bölüm içindeki animasyonlarda görmüş ve hissetmiş olmalısınız. Bu limitler aynı zamanda relativite etkilerinin limitlerini de belirler. Mesela bir saatin tik-tak aralığının uzaması ancak iki katına kadar mümkündür diyebiliriz.

(*) Alice Eşitliği bölümüne bakınız.

Figür 7, Doppler Efekti ve Kuvvet Etkisi

Kuvvet etkisindeki hareketlerde hız değeri değiştiği için kolaylıkla tahmin edileceği gibi Doppler Etkisi zamana göre artar veya azalır. Grafiklerde bu durumu görüyoruz.

Şimdi burada gerçekten çok ilginç bir yere geldik. Çünkü geldiğimiz bu yer GENERAL RELATIVITE dir. (c+v)(c-v) matematiğine kuvvet etkisini ilave ederek genelleştirmek Genel Relativite demektir. Bu sayfadaki grafik General Relativitenin ne olduğunu bize gösteren çok güzel bir örnektir. Bundan sonra Genel Relativite bu kadar basit olacaktır.

Yolumuza Alice Eşitliği bölümüyle devam edeceğiz.

aliceinphysics.com

Establish: December 2001